Why the Inverse of a Function exists only if it is a One-to-One and Onto Function?
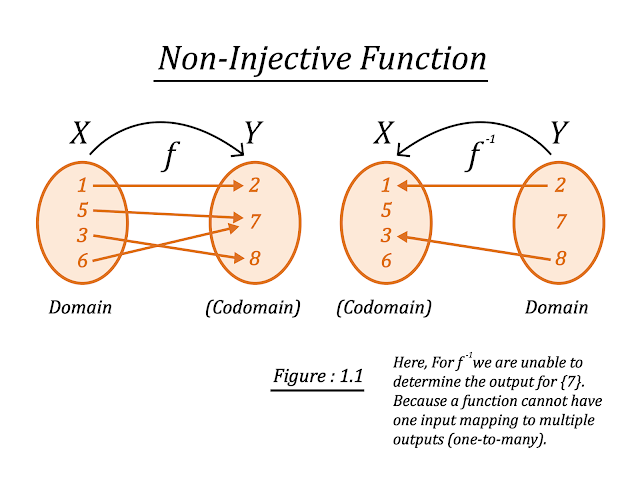
Non-Injective = Not One-to-One
The Inverse of a Function exists only if the Function is One-to-One because the Inverse of a Function needs to uniquely reverse the original Function's mappings. If the Function isn’t one-to-one, it means that multiple inputs in the domain will produce the same output in the codomain. This makes it impossible to determine a unique input for a given output when trying to find the inverse. In this case, the given Function may still satisfy the definition of a Function, but when we take the Inverse of that Function, it will violate the definition.
As you can see in the above Figure : 1.1, we are unable to determine the Inverse of that Function completely. For {7} we have two options, one is to map it to {5}, and the other is to map it to {6}. So, we don't know which one is the correct mapping. If we map it to both, the mapping becomes one-to-many and whenever this happen it violates the definition of a Function, because a function can never be one-to-many.
That's why, it is essential for a Function to be both One-to-One and Onto in order to have an inverse. Otherwise, Inverse of a Function is not possible.
If a Function is One-to-One but Into, the same situation occurs. As shown in Figure : 1.2, when we try to find the Inverse of a Function, there will be no output mapping for {4}. Now you know that a function must not only be One-to-One but also Onto.
As shown in Figure 1.3, every element in the Codomain has a corresponding unique element in the domain. This ensures that the inverse of the Function can be defined for every output.
Each element in the codomain has a unique Pre-Image in the Domain, allowing us to reverse the mapping without any difficulty. This is the key characteristic that makes the inverse of a One-to-One and Onto Function well-defined and achievable.










0 Comments